わり算の世界を広げよう 割進めることができるわり算
公開日: 2024年7月10日水曜日
子どもたちの問題を見ていると、わる数が小数の問題や小数÷小数の問題をつくっているのですが、わる数とわられる数を2の倍数の関係にしたり、5の倍数を用いたりして、無自覚にもきちんとわりきれる問題をつくっている様子でした。
そこで、単元内において新たな見方・考え方を表出させていくためにも原題として教科書の問題や数値設定を織り交ぜながら子どもたちに提示してきています。
今回の学習課題については、特に前時では等分除である概数を取り扱った問題、そして次の時間は包含除で同じように概数表記してしまうと問題の文脈に合わなくなってしまう問題と意図された場面設定と数値設定がなされています。
子どもたちも問題づくりを単元の中でおこなってきたからこそ、子どもたちの思いとそこに教科書の意図も組み合わせながら、より深い学びへと誘っていけるように単元を再構成しながら学び進めているところです。
またこれまで同様、廊下にある道具を題材にした問題を扱うことで、子どもたちは問題づくりで触れてきているためにすぐにイメージができたり操作しながら考えることができたりするようにしています。
まずはこの問題を提示しました。
C「式は2.5÷1.5になります。」
T「どうしてわる数が1.5になったの?」
C「1Lの重さを聞いているからです。」
C「この問題は1.5÷2.5にならないかな?」
C「それだと、1kgあたりの量になるよ。」
今までの学習経験を活かし、等分除の問題のわる数が表す意味について立ち止まりながら考える姿がありました。
子どもたちはそこから自力解決の時間に移りました。
いっときして、子どもたちは思い思いに呟き始めました。
以下は同時多発的にそれぞれで対話が起こっていました。今、どの子どもたちの中にも絶対的な解をもたない瞬間ができています。ここでの対話を今年度の算数科では数学的コミュニケーションと位置付け、研究を進めています。
C「この問題は無理じゃない?」
C「割り切れないよ。」
C「うまく求められない。」
C「やっぱり1.5÷2.5なんじゃないかな。」
C「概数?」
C「あまり?」
C「どうすればいいんだろう・・・」
C「答えは0.6なんじゃない?」
子どもたちそれぞれの言葉がさらに大きくなり、ほとんどの子どもたちが自分自身にとっての解をもち始めた状態を見取り、全体に問いかけました。
T「何を困ってるのかな?」
C「2.5÷1.5が1.66666・・・になるし、1.5÷2.5は0.6になって0.6kgでうまく表せないんじゃない?」
C「1.6666・・・は無限に答えが続いてしまうし、逆に0.6Lでもうよくわからなくなってしまうよ。」
ここで、筆算の解き方を共有しました。
C「ここにまた100がきているから、この後も6が続くことがわかります。だから概数で表せないかと考えました。」
C「おーすごい!」
C「1.66666667なんじゃないかな。」
C「なんでそうなったかわかります。」
C「まず、問題の答えは1.6666・・・で続いてしまうけど、続いてしまうから4年生の時に習ったやつみたいに、四捨五入をして、5より大きい数は切り上げをします。だから最後が7になってるんだと思います。」
C「それなら1.7にした方が・・・」
ここで一度問題文に戻って、どの概数を適用すべきか対話を焦点化しようとしました。
T「この問題は何を求めてるの?」
C「1Lの重さを求めています。」
C「一生求められないよ。」
C「そういう時は四捨五入するという手があります。」
T「どこで四捨五入すればいいと思う?」
C「小数第2位がいいと思います。1.7にすればいいです。」
C「それは小数第2位を四捨五入しなさいということだね。」
C「1.666と続くから1.67までは表しておくべきだと思う。」
C「いずれにしても、約という言葉は絶対に必要だね。」
子どもたちにとって、初めは数人しか働かせていなかった概数の見方について、それぞれが働かせている数学的な見方・考え方を織り交ぜながら対話を進めていくうちに、この時間における数学的価値として大切なものと実感している様子がありました。
C「問題としては、概数で表しなさいという言葉があると親切になります。」
C「小数第何位までという言葉もあるといいね。」
ここで問題文をもう一度見直し、つくりかえていくことで、概数で答えを表す必要がある問題づくりの視点を共有しました。これは子どもたちと問題づくりをしてきたという学びの文脈だからこそ、出てくる発言であるように感じています。
この時間にも問題づくりを行いました。
この時間の問題づくりの時間は、青のカード(問題カード)からというより、赤のカード(解き方カード)で数値設定をした後に問題文をつくる姿が多く見られていました。
今までは出なかった意図的な数値設定をする子どもの姿も見られました。
このように、7でわるわり算の問題も出てきています。3や7でわると今回のように「一生続く問題」ができる可能性が高いと数学の世界の中で考察を進めている子どもの様子もありました。また、わりきれないわり算の問題について、算数図日記においても「長く続く問題は答えを四捨五入すればいい」というような振り返りを書く子どもが多くいました。多くの子どもたちにとって、この時間で働かせていた数学的な見方・考え方の中からこの「概数で表すことができる」ということを、数学的価値として実感したものであったようです。
次の時間はわり算の世界を広げようの最後の時間になります。
最初に述べたように、わり切れない包含除の問題(商が循環小数の問題を取り扱う予定です。)割り切れないときは概数で表せばいいと学んだ子どもたちが、問題文に返ったり、実際に操作してみたりする中で「今回も本当に概数で表していいのか」と自ら立ち止まる姿を生み出していけたらと思っております。
わり算の世界をどんどん広げ続ける子どもたちの次なる学びがとてもたのしみです。
最後までお読みいただきありがとうございました。
算数科 津川

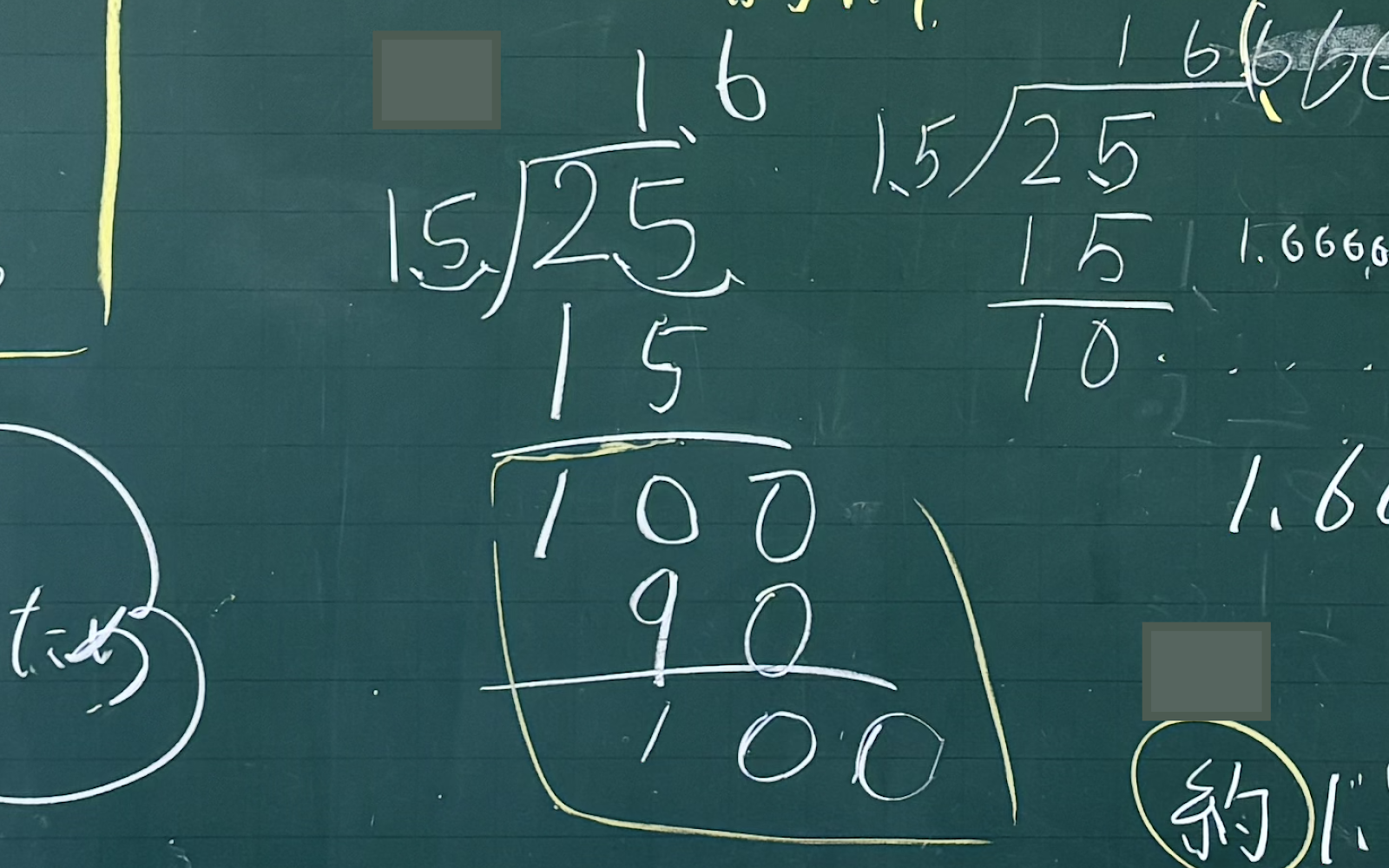



0 件のコメント :
コメントを投稿