６年 比 「くじ引きゲームをプロデュース！」第５時
公開日： 2025年5月21日水曜日
算数科の津川です。
今回は、この色のレシピを提示するところから始めました。
T「この班の色の比を見て気付くことある？」
C「小数点を使ってる」
T「比に小数は出てくるかな？」
C「戻せるよ」
T「小数を戻すってイメージつく？」
C「整数に戻すってことかな？」
C「簡単な整数の比にするってことか」
C「２倍にしたらできそう？」
C「１０倍でもできるよ」
ここから、それぞれ計算する時間をとりました。
上の２つの計算を黒板に書かせました。
まず左側の計算を書かせた際に、自分と比べて「同じ式」という言葉と一緒に「少し違う」という言葉も聞こえてきました。そこで以下のように問いました。
T「何が違うかわかる？」
C「かける数が違うよ」
T「じゃあ、この2つの計算に共通しているところってあるかな？」
C「2つとも整数にしているね」
C「（右側は）×２をしているよ。すぐに整数になってる」
C「小数だと（比を簡単にすることが）できないから整数に直しているね」
１６：３という得られた結果を、色づくりの事象に戻して、意味付けするところまで意識して問いかけました。
T「このことから、この班はどんなことが言えるのかな？」
C「黄色１６滴と青が３滴でも同じ色が作れるということだね」
さらに、小数を整数の比に直すことができるということを確認した上で、以下の２問を解かせました。
この問題を解いている際に、子どもたちに「どのようやって解いたのか」を問うていくことで、その過程の計算を意識させていきました。その中で、どんな数でもできるよという発言があったので、その言葉を基にして全体に問いかけ、立ち止まりを促しました。
T「どんな数でもできるの？」
C「分数でも・・・」
T「分数でもできるの？」
そこで、試しに分数の問題を提示しました。
T「れいとさんは何をしていると思う？」
C「何をしているんだろう・・・」
C「通分？」
C「最小公倍数？」
C「分母を揃えてる」
C「（分母を揃えるということは）これまでと同じように通分して解いたよ」
ここで通分の考え方をおさえた上で、演習問題を１問解かせました。
途中で出てきた比は全て等しい関係にあることもおさえていきました。
そして、分数や小数の比も簡単にすることができることを確認した上で、それぞれオリジナルの色を用いてあたりカードを作っていくことを促しました。
れいと「オリジナルの色ってなんだったっけ？」
しんじ「この前作った色を確認しよう」
なつき「黄色は何滴になったっけ？」
しんじ「６０滴だよ」
しんじ「黄色がちょっと強くなったね」
なつき「青が足りなかったね」
しんじ「色ができたよ」
なつき「オリジナルのマークを作るね」
この班では、たくさんオリジナルの色を用意する必要があるというところから、多めの数を伝えながら色をつくりだしている様子でした。
ここから、上の写真のようにあたりカードを作っていきました。
一度１０枚して考えることに価値を感じているようでした。他のどの問題にも適応できるよさを見いだしているようです。
分数や小数の比を中途半端な比と表現していました。分数の比を簡単な比として表す際に、分数と割合、比の学びを関連させながらまとめる姿が素敵だなと感じました。
等しい比について、分数の計算と関連させながら振り返っています。前の振り返りもそうですが、単元間の見方を統合して捉える姿も価値付けていきたいと思っています。
この子は、この形の図に価値を感じているようです。比の学習に関して、どの問題においてもこの図を応用させて考えようとする姿が見られています。
この考えは、一番最初の小数の比を簡単にした際に、かける数を２した考えから発展しています。より小さい数をかける際にどの数をかけるとよさそうかまとめています。
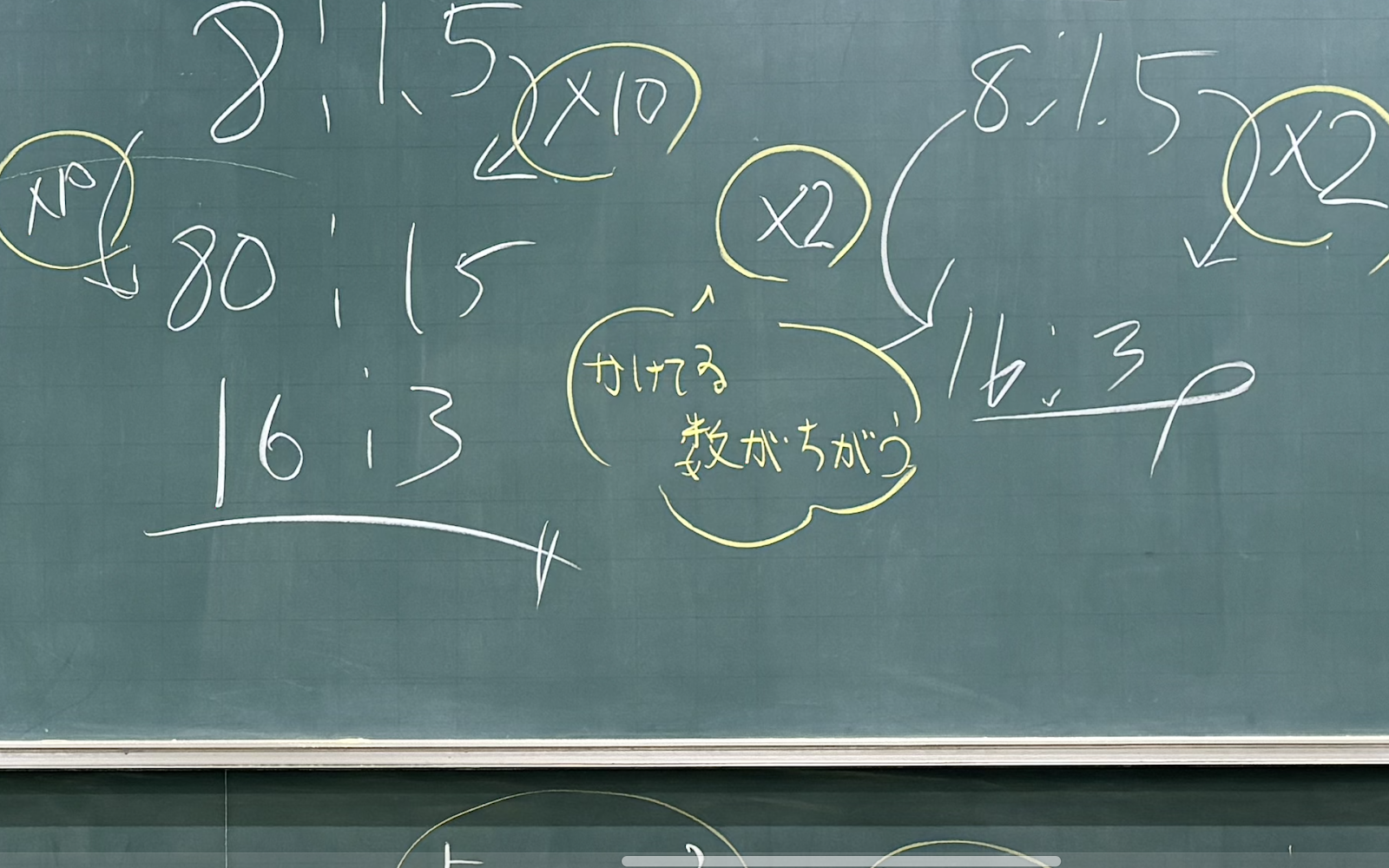
0 件のコメント :
コメントを投稿